Binary Search Tree Iterative Insert

1. BST Iterative Insert Algorithm
2. BST Iterative Insert Illustration
3. BST Iterative Insert Implementation
4. BST Iterative Insert Algorithm Complexity

In the previous article Binary Search Tree, we discussed the recursive approach to insert a node in BST. In this post, we will discuss the iterative approach to insert a node in BST. It is better than the recursive method as no extra space is required by the iterative insertion algorithm.

BST Iterative Insert Algorithm

Let root be the root node of BST and key be the element we want to insert.

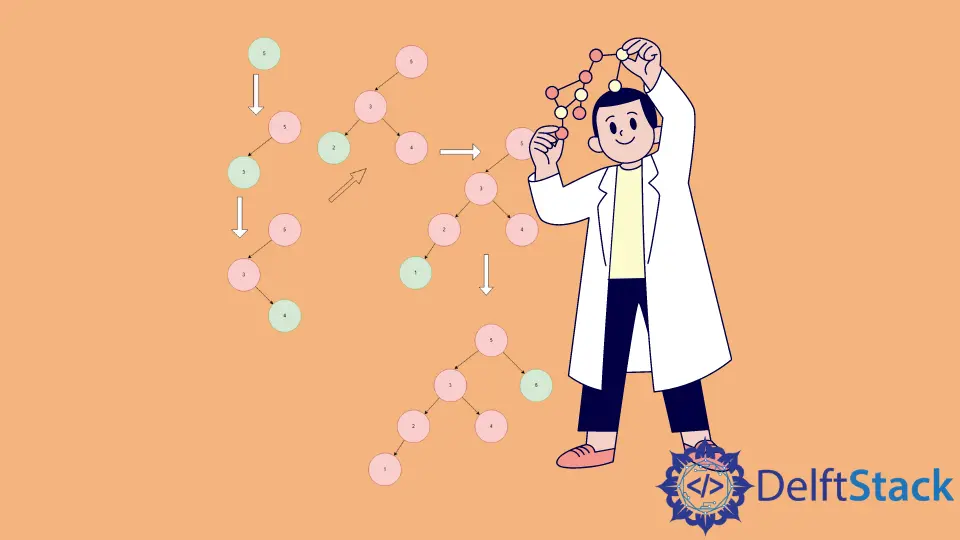
BST Iterative Insert Illustration

This is how we insert elements inside a BST.

BST Iterative Insert Implementation

#include <iostream>
using namespace std;

class Node {
 public:
  int key;
  Node *left, *right;
};

Node *newNode(int item) {
  Node *temp = new Node;
  temp->key = item;
  temp->left = temp->right = NULL;
  return temp;
}

void inorder(Node *root) {
  if (root != NULL) {
    inorder(root->left);
    cout << root->key << " ";
    inorder(root->right);
  }
}

void insert(Node *&root, int key) {
  Node *toinsert = newNode(key);
  Node *curr = root;
  Node *prev = NULL;

  while (curr != NULL) {
    prev = curr;
    if (key < curr->key)
      curr = curr->left;
    else
      curr = curr->right;
  }
  if (prev == NULL) {
    prev = toinsert;
    root = prev;
  }

  else if (key < prev->key)
    prev->left = toinsert;

  else
    prev->right = toinsert;
}

int main() {
  Node *root = NULL;
  insert(root, 5);
  insert(root, 3);
  insert(root, 8);
  insert(root, 6);
  insert(root, 4);
  insert(root, 2);
  insert(root, 1);
  insert(root, 7);
  inorder(root);
}

BST Iterative Insert Algorithm Complexity

Time Complexity

• Average Case

On average-case, the time complexity of inserting a node in a BST is of the order of height of binary search tree. On average, the height of a BST is O(logn). It occurs when the BST formed is a balanced BST. Hence the time complexity is of the order of [Big Theta]: O(logn).

• Best Case

The best-case occurs when the tree is a balanced BST. The best-case time complexity of insertion is of the order of O(logn). It is the same as average-case time complexity.

• Worst-Case

In the worst-case, we might have to traverse from root to the deepest leaf node, i.e., the whole height h of the tree. If the tree is unbalanced, i.e., it is skewed, the tree’s height may become n, and hence the worst-case time complexity of both insert and search operation is O(n).

Space Complexity

The iterative insert operation’s space complexity is O(1) because no extra space is required.