The Diff() Function in MATLAB
This tutorial will discuss finding differences and approximate derivatives using the diff() function in MATLAB.
Find Differences and Approximate Derivatives Using the diff() Function in MATLAB
In MATLAB, the diff() function is used to compute the differences between consecutive elements of an array along a specified dimension. This function is particularly useful for analyzing and understanding the rate of change or discrete derivatives of a sequence of values.
Basic Syntax:
diff(x)
In the syntax, the x is the input vector or matrix.
If the input is a vector, then the difference will be the difference between the vector’s adjacent values. The output vector will be one size smaller than the input vector.
Find the Difference Between the Values of a Vector
Code:
x = [1 3 6 9];
y = diff(x)
In the code, a vector x is defined with values [1, 3, 6, 9]. The diff() function is then applied to the vector x, which calculates the differences between consecutive elements.
The result is stored in a new vector y.
Output:
y =
2 3 3
In the output, the differences between adjacent values in x are computed, resulting in a new vector y with elements [2, 3, 3]. If the input is a matrix, then the difference will be the difference between the rows of the input matrix, and the size of the rows will be equal to the difference between the length of the rows and the order of the difference.
Find the Difference Between the Values of a Matrix
Code:
x = [1 3 6 8; 1 2 3 4]
y = diff(x)
In this code, a matrix x is defined with two rows and four columns. Each row represents a sequence of numerical values.
The diff() function is then applied to the matrix x, calculating the differences between consecutive elements along each row. The result is stored in a new matrix y.
Output:
x =
1 3 6 9
1 2 3 4
y =
0 -1 -3 -4
In the output, the differences are computed between the columns of each row, producing a matrix y with elements [0 -1 -3 -4]. If we increase one row in the input matrix, one row will also increase in the output matrix.
Find the NTH Order Difference Between the Values of the Above Vector
We can also find the nth time difference between the vector or matrix elements using the second argument of the diff() function. For example, let’s find the 2nd-order difference between the values of the above vector.
Code:
x = [1 3 6 9]
y = diff(x,2)
In this code, a vector x is defined with values [1, 3, 6, 9].
The diff() function is then applied to the vector x, with an additional argument 2 specifying the order of the difference. This means the function computes the second-order differences between consecutive elements in the vector.
The result is stored in a new vector y.
Output:
x =
1 3 6 9
y =
1 0
In the output, the second-order differences are computed, resulting in a vector y with elements [1, 0]. In the case of higher-order, the diff() function calls itself recursively to find the difference.
Find the Difference Between Columns of the Above Matrix
We can also find the difference between the columns of a matrix instead of the row using the third argument of the diff() function. For example, let’s find the difference between the columns of the above matrix.
Code:
x = [1 3 6 8; 1 2 3 4]
y = diff(x,1,2)
In this code, a matrix x is defined with two rows and four columns, representing two sequences of numerical values.
The diff() function is then applied to the matrix x, with additional arguments 1 and 2 specifying the order of differences along the rows and columns, respectively. This means the function computes differences between consecutive elements along each row, resulting in a new matrix y.
Output:
x =
1 3 6 8
1 2 3 4
y =
2 3 2
1 1 1
In the output, the differences between adjacent columns are calculated, producing a matrix y with elements [2 3 2; 1 1 1]. In case of difference between columns, the size of the columns will be equal to the difference between the length of columns and order of difference, and the row size will remain the same.
Find the Partial Derivative of a Function
We can also find the partial derivative of a function using the diff(f)/h function. Where f is the given function and h is the step size.
For example, let’s find the partial derivative of sin(x) and plot it on a graph using the plot() function.
Code:
h = 0.001;
x = -2*pi:h:2*pi;
f = sin(x);
y = diff(f)/h;
plot(x(:,1:length(y)),y,x,f)
legend('sin(x)','cos(x)')
In this code, a step size h is set to 0.001, defining an increment for the variable x. The vector x is then created with values ranging from -2π to 2π at intervals of h.
The sin(x) function is applied to generate a corresponding vector f. Subsequently, the diff() function is used to compute the derivative of the sine function by dividing the differences in f by the step size h, resulting in a new vector y.
Finally, the plot() function is utilized to visualize both the sine and cosine functions on a graph, with legends indicating their respective plots.
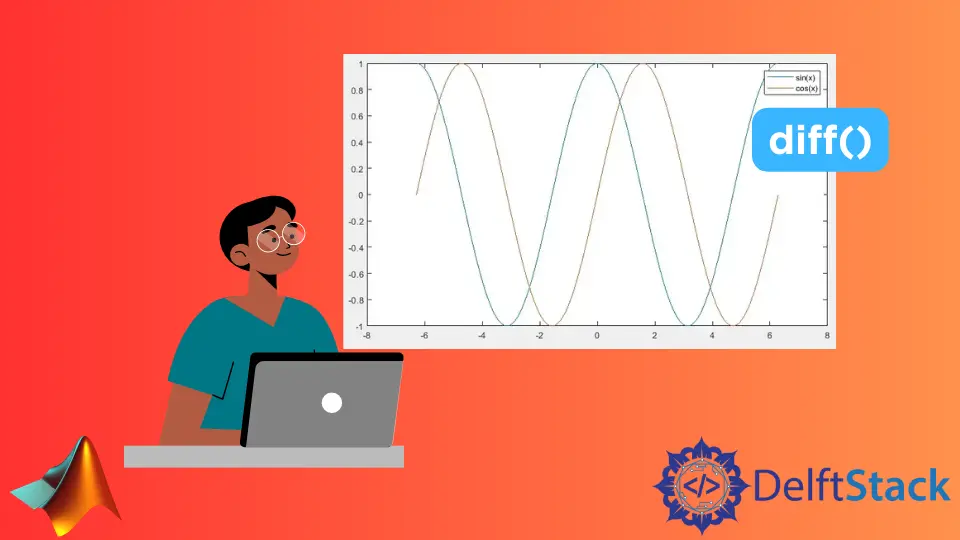
Output:

In the output, the blue line is the sine wave, and the red line is the cosine wave, which is the derivative of the sine wave. The legend() function is used to draw legends on the graph to indicate which plot belongs to which data.
Conclusion
In conclusion, the diff() function in MATLAB proves to be a versatile tool for computing differences and approximate derivatives in sequential data. Whether applied to vectors, matrices, or nth-order differences, this function efficiently captures the nuances of data behavior.
The ability to find differences between columns in a matrix further enhances its utility. In practical applications, such as computing partial derivatives, diff() shines, making it an invaluable asset for scientific computing and data analysis tasks.
