How to Convert a Binary to Decimal in C

1. Convert Binary to Decimal in C
2. Method 1: Convert Using Loop and Integer Variables
3. Method 2: Use a Procedural Approach
4. Method 3: Use the char Array to Store Binary Number

This article comprehensively discusses multiple C implementations to convert binary numbers into decimal equivalents. However, we must look for inevitable conversion foundations before jumping into the implementations.

Convert Binary to Decimal in C

Binary numbers can contain only two values: 0 and 1. However, the decimal notation has ten symbols: 0 through 9 (0,1,2,3,4,5,6,7,8,9).

The binary (0,1) notation is native to computer hardware, while decimal values are the integer values that humans can understand easily.

Conversion Method

The binary number 0101 is equivalent to 5 in decimal. The binary-to-decimal conversion method is quite straightforward, as described by the following formula:

Here B is the full binary number, and B_{i} represents the i^th^ bit in the given binary number. The n represents the total number of bits in the given binary number.

Let’s apply the above formula to a binary number 0101. Taking the summation from left to right, we get:

Binary language is used on the hardware side because there are signals and logic gates in an electronic circuit; it is easily understandable by the system. Every single binary number 0 or 1 is known as 1-bit.

Algorithm to Convert Binary Number to a Decimal Equivalent

Let’s look at a step-by-step procedure to solve this conversion problem.

1. Start the program.
2. Take a binary number as input.
3. If the number is greater than 0, divide the number by ten and take the product of the remainder with 2*i, where i starts from zero.
4. Continue dividing the quotient as discussed in step 3 and increment i by one in each iteration.
5. Add up all the products and return the results.

There are multiple implementation choices to cater to the problem. Let’s start discussing these approaches one by one.

Method 1: Convert Using Loop and Integer Variables

The for and while loops can convert binary to decimal.

Use while Loop

In this approach, the division operation will convert binary to decimal.

#include <math.h>
#include <stdio.h>
int main() {
  int binary_number;
  printf("Enter Binary number: ");
  scanf("%d", &binary_number);
  int decimal = 0, temp = 0, reminder;
  while (binary_number != 0) {
    reminder = binary_number % 2;
    binary_number = binary_number / 10;
    decimal = decimal + reminder * (int)pow(2, temp);
    temp++;
  }
  printf("Decimal number is : %d", decimal);
  return 0;
}

The first line in main() declares a variable named binary_number to take binary input. After taking input for binary numbers, we are further declaring the three variables:

1. decimal: to store the resultant decimal value
2. temp: to serve as an iteration counter
3. remainder: to store the remainder in each iteration

In each while loop iteration, we first determine the rightmost bit from the binary_number and save it in the remainder variable.

Then, we divide the binary_number by ten and overwrite the resultant to itself. This causes the binary_number to lose its rightmost bit.

Moreover, as discussed at the start of the article, we apply the formula to aggregate the weighted products in the decimal variable. In the end, we print the resultant decimal equivalent.

Let’s look at the output.

Use for Loop

The basic structure of both loops (for and while) are similar. The advantage of using a for loop is the straightforward declaration and initialization of the variable in a single line.

Here is another program to convert the binary numbers to decimal values using the for loop.

#include <stdio.h>
int main() {
  int binary, decimal = 0, base = 1, remainder, temp;
  printf("Enter binary number: ");
  scanf("%d", &binary);
  for (temp = binary; temp > 0; temp = temp / 10) {
    remainder = temp % 2;
    decimal = decimal + remainder * base;
    base = base * 2;
  }
  printf("Decimal number is:%d", decimal);
  return 0;
}

In the for loop implementation, we used a slightly different approach than in the while loop.

Instead of using a costly pow() function, we just created a variable base that will multiply itself with a value of 2 in each iteration. This will ensure that at the start of the i^th^ iteration, the base variable has a value equivalent to 2^i^, where i starts from zero.

Output:

Method 2: Use a Procedural Approach

This method will use a user-defined procedure or function to solve the conversion problem. This approach is the most desirable if you want to make your code more reusable and modular.

#include <math.h>
#include <stdio.h>
int binarytodecimal(int binary_number) {
  int decimal = 0, temp = 0, remainder;
  while (binary_number != 0) {
    remainder = binary_number % 2;
    decimal = decimal + (remainder * pow(2, temp));
    binary_number = binary_number / 10;
    temp++;
  }
  return decimal;
}

int main() {
  int binary_number, decimal;
  printf("Enter binary number: ");
  scanf("%d", &binary_number);
  decimal = binarytodecimal(binary_number);

  printf("Decimal Number is: %d", decimal);
  return 0;
}

Everything is the same as our previous method except that we enclosed the whole conversion code to a single procedure, binarytodecimal().

Method 3: Use the char Array to Store Binary Number

In all the earlier discussed methods, the major issue is the size of the integer. We were storing binary numbers in integer encoding.

So, for a 16-bit compiler, the largest number we could provide was 111111.

The 32-bit and 64-bit compilers with larger integer sizes will surely increase the input range and solve the problem. However, the issue will scare us in the older versions.

Fortunately, we have a hack to cater to the problem, i.e., use a dynamic char array to store binary numbers instead of the integer variable. Let’s look at the following code to understand the strategy.

#include <conio.h>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
int main() {
  long decimal = 0;
  int size;
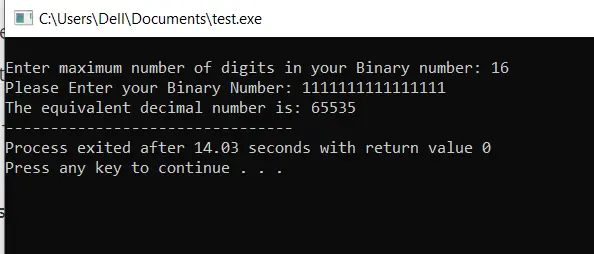
  printf("\nEnter maximum number of digits in your Binary number: ");
  scanf("%d", &size);

  char* BinaryArr = (char*)malloc(size + 1);

  printf("Please Enter your Binary Number: ");
  scanf("%s", BinaryArr);

  char ch;
  for (int i = size - 1, j = 0; i >= 0; i--, j++) {
    ch = BinaryArr[i];
    decimal += atoi(&ch) * (int)pow(2, j);
  }

  printf("The equivalent decimal number is: %d", decimal);
  return 0;
}

We first ask the users to confirm the size of the binary number that they want to convert into a decimal equivalent.

Given that we know the size of the binary number, we dynamically allocate an array of that size using the malloc() function. The malloc() is defined in stdlib.h and allocates dynamic memory in bytes.

To make it a character array, we explicitly type-casted the return pointer of malloc() to a char* type.

Note: The extra 1 in malloc(size +1) is because we want space to store the \0 character at the end.

Next, we take the binary number as input in the character array pointed by the character pointer BinaryArr.

After that, we start iterating this character array from the last index (i.e., the least significant bit of the binary number) and take binary characters one by one moving nearer to the index 0 after each iteration.

We store the i^th^ index in an auxiliary ch variable in each iteration. Then, we apply the atoi() function to get an equivalent integer value.

Then, we put everything into the formula discussed at the start of this article.

Finally, soon as the loop terminates, we print the final decimal value. Let’s see how it feels on the output console.